파이프 옮기기 1

📑
Baekjoon 17070번, 파이프 옮기기 1

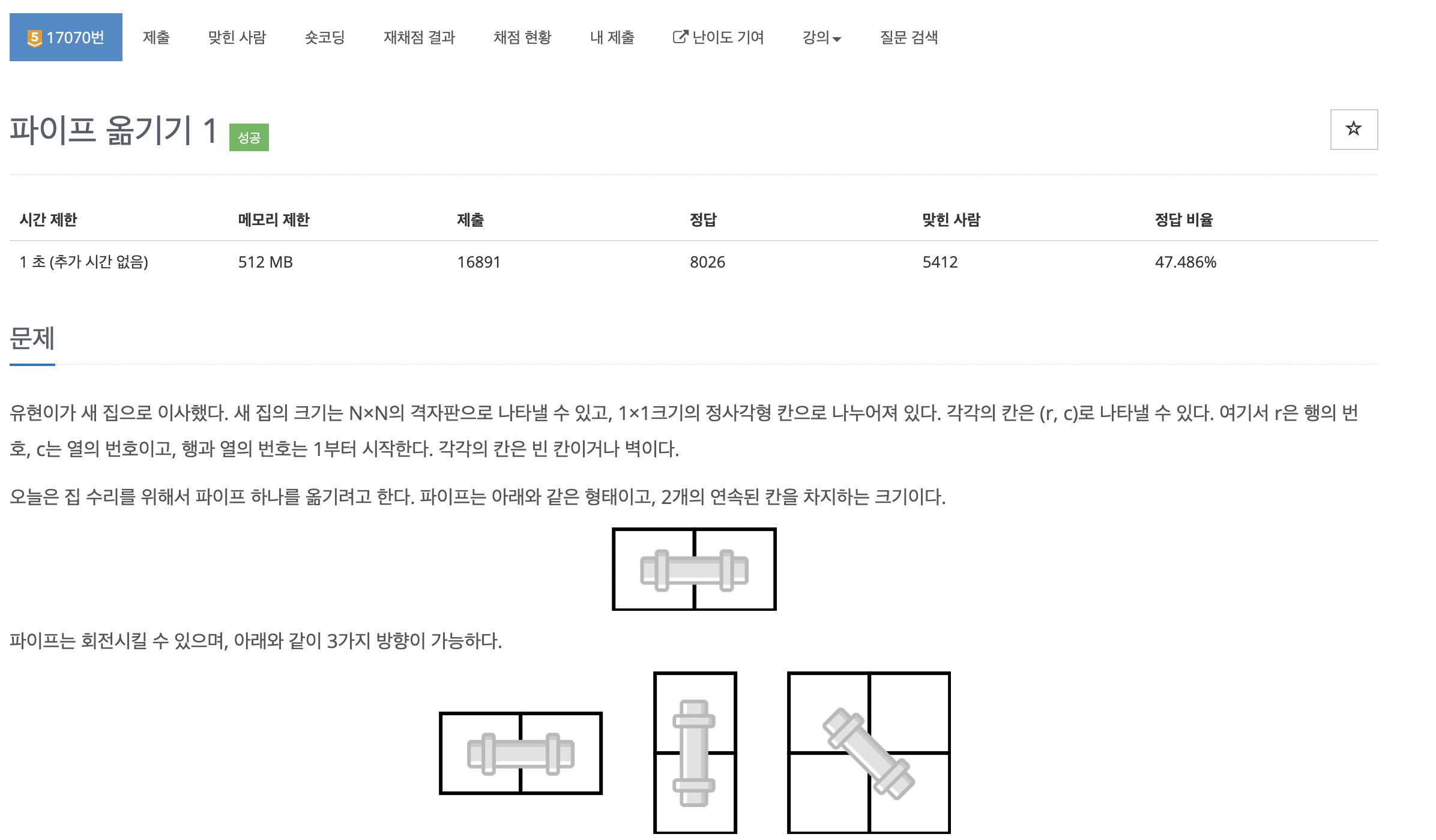
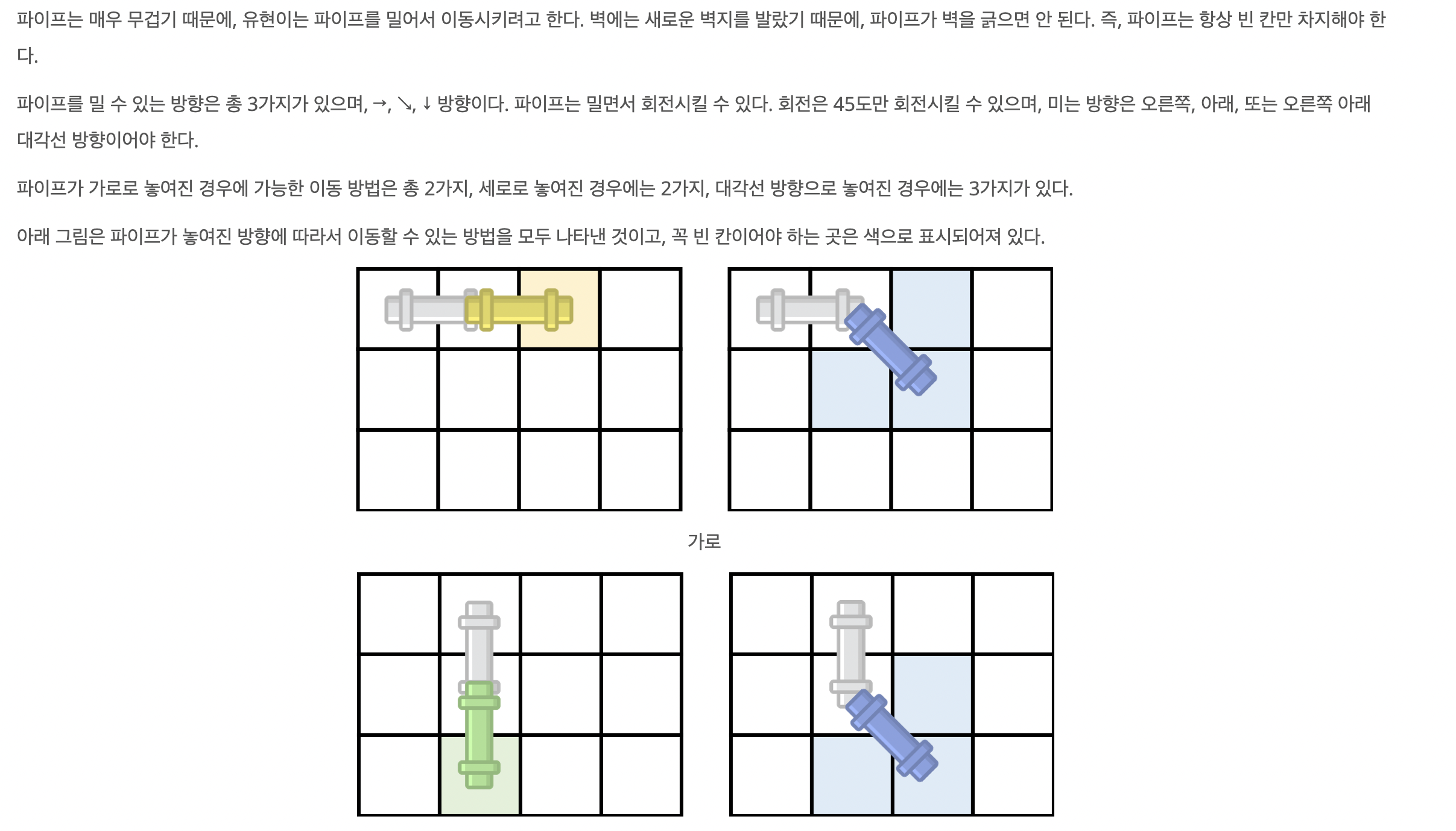
🤔 dp 이용하기

dp[i][j][k] = 방향이 i이고 파이프 앞쪽이 (j,k)에 올 수 있는 경우의 수

🧐 구현 방법

1. 초기화하기 1-1. 가로 방향으로 앞쪽이 (1,2)에 올 수 있는 경우는 항상 1개이다. 1-2. 가로 방향으로 앞쪽이 벽이 아닌 (1,j)에 올 수 있는 경우는 (1,j-1)에서의 경우와 같다.
2. (i,j)가 벽이 아닐 경우, 가로 방향으로 앞쪽이 (i,j)에 올 수 있는 경우는 (가로 방향으로 (i,j-1) 경우 + 대각선 방향으로 (i,j-1) 경우)의 합이다.
3. (i,j)가 벽이 아닐 경우, 세로 방향으로 앞쪽이 (i,j)에 올 수 있는 경우는 (세로 방향으로 (i-1,j) 경우 + 대각선 방향으로 (i-1,j) 경우)의 합이다.
4. (i,j), (i-1,j), (i,j-1)이 벽이 아닐 경우, 대각선 방향으로 앞쪽이 (i,j)에 올 수 있는 경우는 (가로 방향으로 (i-1,j-1) 경우 + 세로 방향으로 (i-1,j-1) 경우 + 대각선 방향으로 (i-1,j-1) 경우)의 합이다.
5. 앞쪽이 (n,n)에 올 수 있는 경우는 dp[가로][n][n] + dp[세로][n][n] + dp[대각선][n][n] 의 합이다.

✏️ 구현 코드(python) ✏️

import sys
from collections import deque

HORIZONTAL = 0
VERTICAL = 1
DIAGONAL = 2

def get_case(graph, dp, n):
    if graph[n][n] == 1:
        return 0
    dp[HORIZONTAL][1][2] = 1
    for j in range(3, n+1):
        if graph[1][j] == 0:
            dp[HORIZONTAL][1][j] = dp[HORIZONTAL][1][j-1]
    for i in range(2, n+1):
        for j in range(3, n+1):
            if graph[i][j] == 0:
                dp[HORIZONTAL][i][j] = dp[HORIZONTAL][i][j-1] + dp[DIAGONAL][i][j-1]
                dp[VERTICAL][i][j] = dp[VERTICAL][i-1][j] + dp[DIAGONAL][i-1][j]
            if graph[i][j] == 0 and graph[i-1][j] == 0 and graph[i][j-1] == 0:
                dp[DIAGONAL][i][j] = dp[HORIZONTAL][i-1][j-1] + dp[VERTICAL][i-1][j-1] + dp[DIAGONAL][i-1][j-1]

    return dp[HORIZONTAL][n][n] + dp[VERTICAL][n][n] + dp[DIAGONAL][n][n]


n = int(sys.stdin.readline())
graph = [ [1]*(n+2) for _ in range(n+2) ]
temp = []
for _ in range(n):
    temp.append(list(map(int, sys.stdin.readline().split(' '))))
for i in range(1, n+1):
    for j in range(1, n+1):
        graph[i][j] = temp[i-1][j-1]
dp = [ [[0]*(n+2) for _ in range(n+2)] for _ in range(3)]
print(get_case(graph, dp, n))