Ella 
📚
개념 3️⃣ Tree
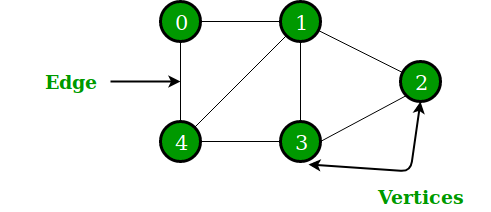
트리(tree)는 계층적인 자료를 표현하는데 이용되는 자료구조이다. 계층적인 자료구조에는 컴퓨터의 디렉토리 구조, 인공 지능의 결정 트리(decision tree) 등이 있다.
트리의 용어
(1) 트리
✏️ 한 개 이상의 노드로 이루어진 유한 집합
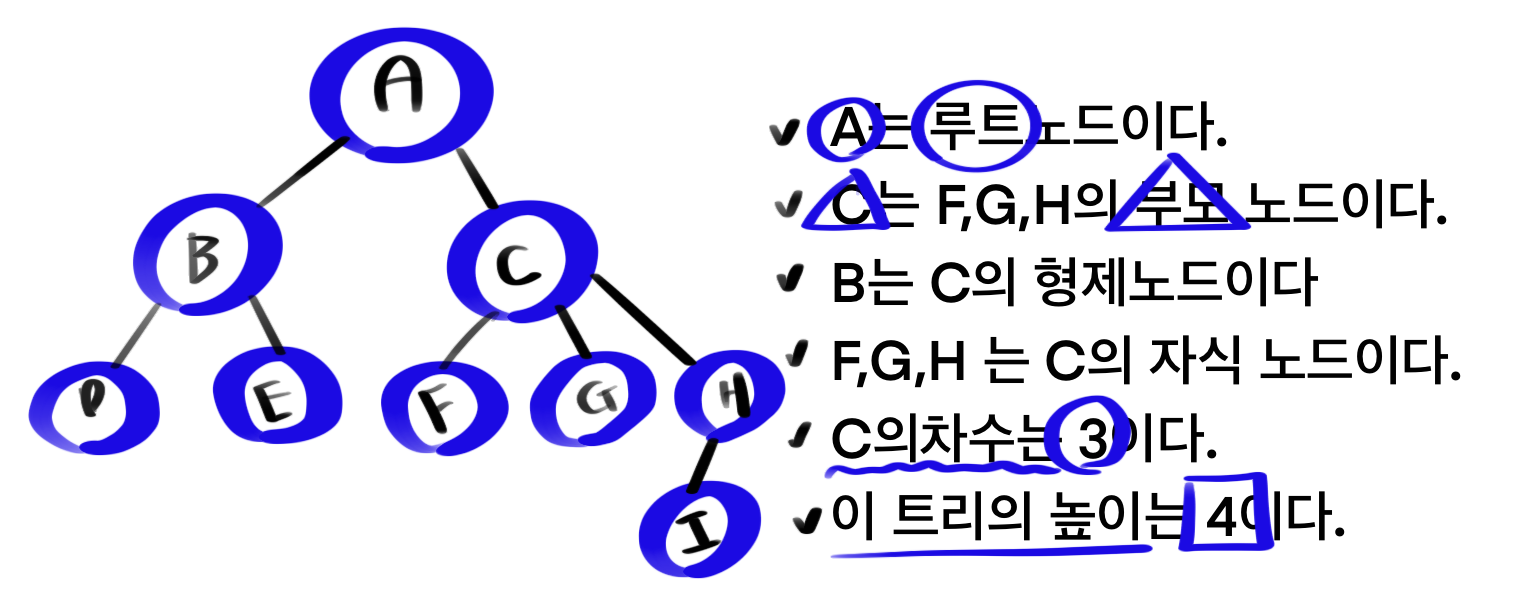
(2) 루트(root) 노트
✏️ 가장 높은 곳에 있는 노드
(3) 서브트리(subtree)
✏️ 루트 노드를 제외한 나머지 노드
(4) 간선 또는 엣지(edge)
✏️ 루트와 서버트리를 연결하는 선
(5) 부모 노드(parent node)
✏️ 두 노드의 관계에서 위에 있는 노드
(6) 자식 노드(children node)
✏️ 두 노드의 관계에서 아래에 있는 노드
(7) 단말 노드(terminal node 또는 leaf node)
✏️ 자식 노드가 없는 노드
(8) 비단말 노드(nonterminal node)
✏️ 자식 노드가 있는 노드
(9) 노드의 차수(degree)
✏️ 어떤 노드가 가진 자식 노드의 개수
(10) 트리의 차수
✏️ 트리가 가진 노드의 차수 중에서 가장 큰 차수
(11) 레벨(level)
✏️ 트리의 각 층에 번호를 매기는 것
(12) 트리의 높이(height)
✏️ 트리가 가지고 있는 최대 레벨
이진트리(Binary Tree)
- 모든 노드가 2개의 서브트리를 갖는 트리
- 서브트리는 공집합있을 수도 있음
- 따라서 모든 노드의 차수는 2이하이며 최대 2개까지의 자식노드를 가질 수 있음
이진트리의 순환적 정의
(1) 공집합이거나
(2) 루트와 왼쪽 서브트리, 오른쪽 서브트리로 구성된 노드들의 유한 집합
(3) 이진트리의 서브트리들은 모두 이진트리여야 함
이진트리의 특징
- n개의 노드를 가지는 이진트리는 n-1개의 간선을 가짐
- 높이가 h인 이진트리는 [h개 이상 ~ 2^k-1개 이하] 개수의 노드를 가짐
- 각 레벨에 하나씩만 있으면 h개
- 각 레벨에 꽉꽉 채워져 있으면 2^k-1개
포화 이진트리(full binary tree)
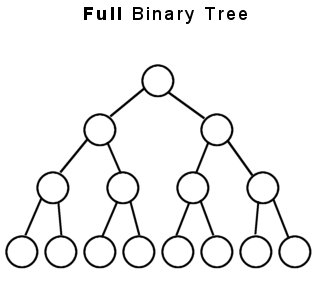
- 트리의 각 레벨에 노드가 꽉 차 있는 이진트리
- 높이 k인 포화이진트리는 2^k-1개의 노드를 가짐
완전 이진트리(comblete binary tree)
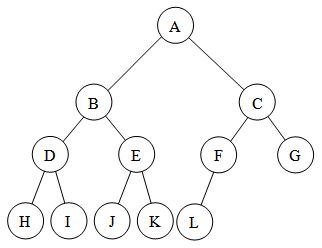
- 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리
- 높이가 k인 트리에서 레벨 1부터 k-1까지는 노드가 모두 채워져 있음
- 마지막 레벨은 노드가 꽉 차있지는 않더라도 중간에 비어있으면 안됨
- 포화 이진트리는 항상 완전 이진트리이지만, 완전 이진트리가 항상 포화 이진트리는 아니다.
[참고 사이트 및 서적]
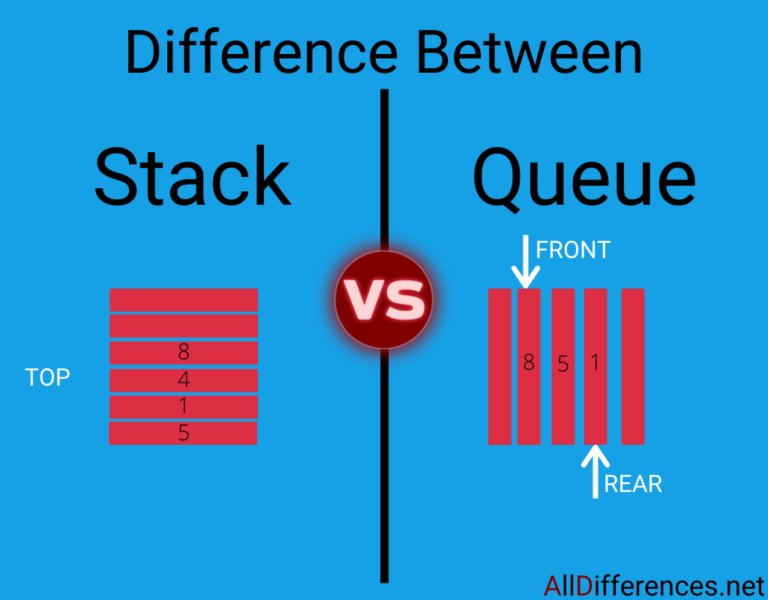Stack과 Queue