Ella 
📚
개념 4️⃣ Binary Heap
힙(heap)은 트리 기반 자료구조로 힙 속성을 만족하는 트리이다. 최대 힙(Max Heap)의 속성은 부모 노드가 자식 노드보다 값이 크다는 것이고, 최소 힙(Min Heap)의 속성은 부모 노드가 자식 노드보다 값이 작다는 것이다. 이러한 힙의 특성으로 힙은 우선순위 큐를 구현하기에 적합한 자료구조이다. 다만, 힙에서는 부모와 자식 노드 간에 크고 작음만 정의되어 있을 뿐, 형제 또는 사촌 노드간의 우선순위는 정의되어 있지 않다.
이진 힙(Binary Heap)이란?
이진 힙(Binary Heap)은 힙 중에서 가장 잘 알려진 형태로, 이진 트리(Binary Tree) 형태인 힙이다. 지난 포스트에서 공부했듯이, 이진 트리는 각 노드의 자식 노드가 2개 이하인 트리이다. 이진 힙이 되려면 ‘완전 이진 트리’여야 한다. 완전 이진 트리는 레벨 k-1까지는 모든 노드가 꽉 차있고, 마지막 k 레벨에서는 왼쪽에서부터 차있는 트리이다.
(1) 삽입
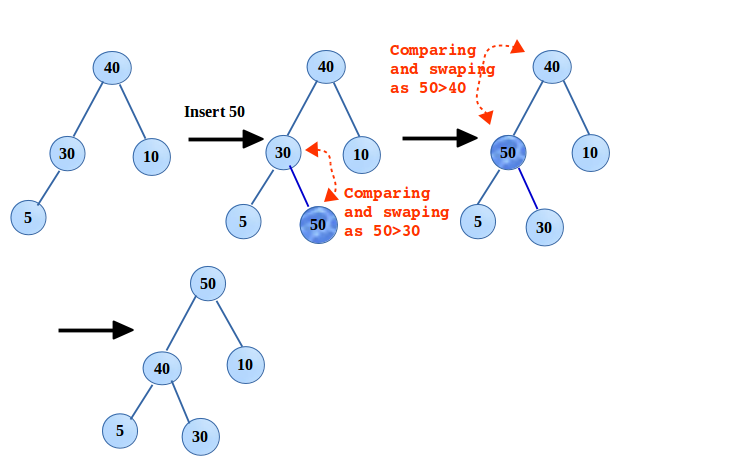
- 힙에 원소를 추가하려면, 업힙을 수행해야 한다.
- 원소를 힙의 가장 마지막 노드에 추가한다.
- 부모노드랑 힙 조건 비교
- 힙 조건이 맞지 않으면, 부모와 자리 바꾸기
- 힙 조건이 맞으면 중지
(2) 삭제
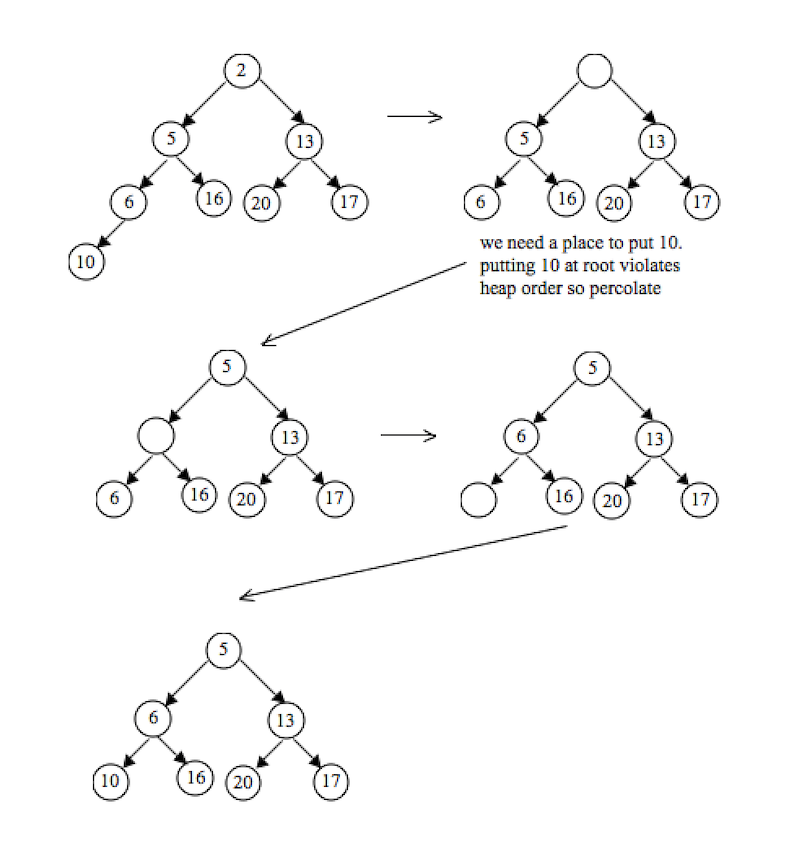
- 힙에서 삭제되는 원소는 최대값 또는 최소값인데 이 값은 루트 노드이므로, 최대값 또는 최소값을 탐색하는데 걸리는 시간은 O(1)이다.
- 힙에 원소를 삭제하려면, 다운힙을 수행해야 한다.
- 루트 노드에 있는 원소를 삭제한다.
- 마지막 노드를 루트로 옮긴다.
- 루트를 자식 노드와 비교한다. 최대 힙인 경우 두 자식 노드 중 더 큰 자식과 비교하고 최소 힙인 경우 두 자식 노드 중 더 작은 자식과 비교한다.
- 힙 조건이 맞지 않으면, 해당 자식과 자리 바꾸기
- 힙 조건이 맞으면 중지
[참고 사이트]
ArrayList와 LinkedList